자료구조란?(Data Structure)
-자료를 효율적으로 관리하기 위한 구조
(여기서 관리란 저장, 삭제, 탐색 등을 말함)
-알고리즘과 밀접한 관계에 있다.
비선형 vs 선형 자료구조
| 선형 자료구조 | 비선형 자료구조 |
| 자료에 순서가 있다.(set, Map은 명시적인 순서x) | 자료에 순서가 없다. |
| 순서를 중요시 하지 않는 자료구조여도, 자연스럽게 읽는 순서(natural order)가 있다. |
단순히 자료를 한번 순회하는 데에도 방법론이 필요하다. (DFS, BFS가 많이 쓰인다.) |
*선형 자료구조:
-배열
-연결리스트
-스택, 큐, 데크
-해시 테이블
*비선형 자료구조:
-트리
-그래프
-힙/우선순위 큐
-트라이
*트리:

-루트 노드를 시작으로, 뻗어 나가는 자료구조
-하나의 노드에서 다른 노드로 이동하는 경로는 유일
-노드가 N개인 트리의 Edge의 수는 N-1 개
-모든 노드는 서로 연결돼 있음
*이진트리(Binary Tree):
각 노드는 최대 2개의 자식을 가질 수 있음
노드는 좌우가 구분됨

| 포화 이진 트리 | 완전 이진 트리 |
| 모든 레벨에서 노드들이 꽉 채워져 있는 트리 (주로 포화 이진트리를 많이 쓴다.) |
마지막 레벨을 제외한 노드들이 모두 채워진 트리 |
*이진 트리의 순회: 모든 노드를 빠뜨리거나 중복하지 않고 방문하는 연산
-순회의 종류:
1.전위 순회(Preorder), 중위 순회(Inorder), 후위 순회(Postorder) ->DFS
2.레벨 순회(level) -> BFS


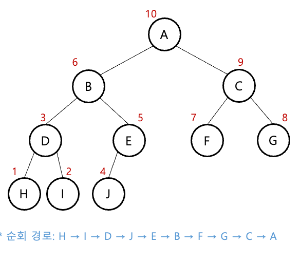
-대표적으로 두 가지 탐색 방법이 사용
1. 깊이우선탐색(Depth-First Search;DFS):
->트리에서 빈출
-찾고자 하는 노드가 리프 노드에 있을 때 사용
-모든 노드를 반드시 다 탐색해야 할 때 사용
2. 너비우선탐색(Breadth-First Search; BFS):
-조건에 맞는 가장 가까운 노드를 찾을 때 사용
-모든 노드를 다 탐색할 필요가 없을 때 사용
*그래프:
-노드와 연결이 자유롭게 이루어지는 자료구조
-트리와 달리 회로(cycle)가 발생할 수 있어 더 복잡(visited 이용하기)
-대표적으로 두 가지 탐색 방법이 사용된다.
1. DFS 2.BFS-> 그래프에선 BFS가 많이 사용
DFS와 BFS 문제의 허들
*DFS:
-재귀 구현을 잘해야 함(스택이용하지 말 것)
-탈출 조건을 잘 이해해야 함(백트래킹 최적화)
*BFS:
-큐를 잘 이해하고 있어야 함
-동적계획법(DF)와 결합되는 경우가 많음
-BFS를 잘 이해해야 Dijkstr 알고리즘 구현가능
비선형 자료구조 학습 순서
1. DFS를 잘 이해한다.
-> DFS 이해가 어려우면 재귀부터 다시 학습
2.BFS를 잘 이해한다.
->BFS 이해가 어려우면 큐 개념부터 다시 학습
3. DFS와 BFS 기초 문제들을 풀이한다.
->백준온라인저지나 프로그래머스 문제 활용
4. 더 난도가 있는 문제들(백트래킹, DP, 비트마스킹, 해싱 이용한) 풀이한다.
5. 고급 알고리즘에 도전한다.
(다익스트라, 벨만-포드 -> 최단거리, 크루스컬, 프림->MST)
오늘 푼 문제(Tree):
//종이접기
//종이를 반으로 접었을 때, 안으로 파인 부분은 0, 볼록 튀어나온 부분은 1이라고 하자.
//종이를 N번 접었을 때의 접힌 상태를 출력하는 문제를 작성하세요.
public class Main {
public static void solution(int n){
int[] binaryTree = new int[(int)Math.pow(2,n)]; //꼭 사이즈 딱 맞추지 않아도 된다.
binaryTree[0] = 0; //root는 무조건 0이기 때문
for (int i = 0; i < (int)Math.pow(2, n-1)-1; i++) {
binaryTree[i*2 +1] = 0; //왼쪽
binaryTree[i*2 +2] = 1;//오른쪽
}
inOrder(binaryTree, 0);
System.out.println();
}
public static void inOrder(int[] arr, int idx){
int left = 2*idx +1;
int right = 2*idx +2;
if (left<arr.length-1){ //배열의 마지막 부분은 사용하지 않기에 -1해줌
inOrder(arr, left);
}
System.out.print(arr[idx]+" ");
if (right< arr.length-1){// 여기도
inOrder(arr, right);
}
}
public static void main(String[] args) {
//Test code
solution(1);
solution(2);
solution(3);
}
}
//각각의 edge에 가중치가 있는 포화 이진 트리가 있다.
//루트에서 각 리프까지의 경로 길이를 모두 같게 설장하고,
//이 때, 모든 가중치들의 총합이 최소가 되도록 하는 프로그램을 작성하세요.
class BinaryTree{
int h;
int[] arr;
int res; //가중치 합을 담을 result
public BinaryTree(int h, int[] w){
this.h = h;
arr = new int[(int)Math.pow(2,h+1)]; //1개는 안씀
res = 0;
for (int i = 2; i < (int)Math.pow(2, h+1); i++) { //i가 2에서부터 시작하는 이유
//맨 앞은 안쓰고, 노드가 아닌 링크(가지)를 세는 것이기 때문에 idx 0,1은 사용하지 x
arr[i] = w[i-2];
}
}
public int dfs(int idx, int h){
if(this.h == h){
res += arr[idx];
return arr[idx];
}
int left = dfs(idx*2, h+1);
int right = dfs(idx*2+1, h+1);
res += arr[idx] + Math.abs(left-right); //Mast.abs -> 절대값 기준
return arr[idx] + Math.max(left, right);
}
}
public class Practice2 {
public static void solution(int h, int[] w){
BinaryTree bt = new BinaryTree(h,w);
bt.dfs(1,0);
System.out.println(bt.res);
}
public static void main(String[] args){
//Test code
int h =2; //트리의 높이
int[] w = {2,2,2,1,1,3}; //트리에서 각각 에지의 가중치
solution(h,w);
System.out.println();
h = 3;
w = new int[]{1,2,1,3,2,4,1,1,1,1,1,1,1,1,1};
solution(h,w);
}
}
마지막 문제 코드의 이해가 어렵고 아직 잘 안된다.
먼저, 트리의 구조를 명시적으로 그리고 어레이에 할당하는 것이 익숙해지게 해야할 거 같다.
DFS를 구현하는 방법을 완전히 이해하기까지 시간이 걸릴 거 같으니,
먼저 코드를 암기하고 문제에 적용하며 익숙해지게 해야할 거 같다.
트리를 구현하는 코드의 앞 부분이 거의 동일하기에,
다시 한 번 문제에서의 트리를 손으로 그려보고, 코드를 구현해야겠다.
순회라는 개념을 글로 보는 것보다, 코드로 구현하는 것이 더 명시적으로 이해가 갔다.
(항상 개념보다 코드 구현이 어려웠는데, 처음으로 코드 구현으로 개념이 이해가 더 갔다.)