그래프(Graph):
-정점과 간선으로 이루어진 자료구조(Cyclic), 연결된 정점간의 관계를 표현할 수 있는 자료구조
-그래프의 용도: 지하철 노선도, 통신 네트워크, ...
-그래프 용어:

-그래프 vs 트리:
| 그래프 | 트리 | |
| 개요 | 노드와 간선으로 이루어진 자료구조 | 그래프의 한 종류 |
| 방향성 | 방향 그래프, 무방향 그래프 둘 다 | 방향 그래프 |
| 사이클 | Cyclic | Acyclic |
| 모델 | 네트워크 모델 | 계층 모델 |
| 루트 노드 | 루트 노드 X | 최상위 노드 |
| 부모-자식 | X | 인접한 상하위 노드 |
| 간선 수 | 그래프에 따라 다름 | N-1개 |
| 순회 | DFS, BFS | Pre-,In-, Post-order/ Level-order |
| 경로 | 2개 이상의 경로 가능 | 두 노드 간의 경로는 오직 1개 |
트리는 그래프의 한 종류이다!
-그래프의 종류:
1. 무방향 그래프: 간선에 방향이 없는 그래프(양방향 이동 가능)
정점 A-B 간선의 표현 : (A,B) =(B, A)
2. 방향 그래프: 간선에 방향이 있는 그래프(해당 방향으로만 이동 가능)
정점 A-> B 간선의 표현 : <A,B> =! <B,A>
(예시는 위에서)
-그래프 탐색 - DFS:
각 노드에 방문했는지 여부를 체크할 배열과 스택을 이용해 구현(선입후출)
-BFS:
각 노드에 방문했는지 여부를 체크할 배열과 큐를 이용해 구현(선입선출)
-그래프의 구현:
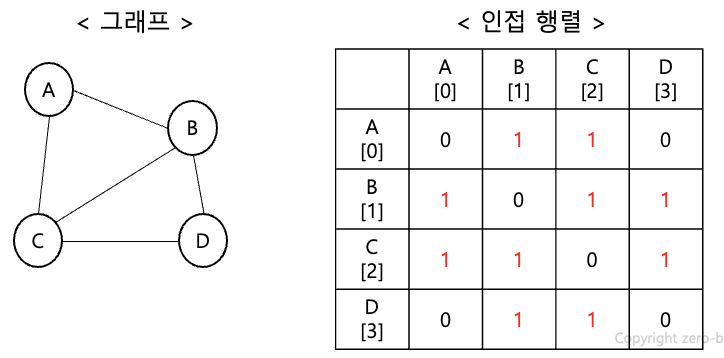
1. 인접 행렬:
-2차원 배열 이용
-장단점:
장점: 간선 정보의 확인과 업데이트가 빠름(복잡도: O(1)) -> 바로 확인, 업데이트
단점: 인접 행렬을 위한 메모리 공간 차지
2. 인접 리스트:
-연결리스트 이용
-장단점:
장점: 메모리 사용량이 상대적으로 적고(인접 행렬보다), 노드의 추가, 삭제가 빠름
단점: 간석 정보 확인이 상대적으로 오래 걸림

행렬 vs 인접 리스트:
| 인접 행렬 | 인접 리스트 | |
| 특정 간선 검색 | O(1) | O(degree(V)) |
| 정점의 차수 계산 | O(N) | O(degree(V)) |
| 전체 노드 탐색 | O(N^2) | O(E) |
| 메모리 | N x N | N + E |
N: 전체 정점 개수, E: 전체 간선 개수
노드의 개수가 적고 간선의 수가 많을 땐 인접 행렬,
노드의 개수가 많고 간선의 수가 적을 땐 인접 리스트가 유리하다!
비선형 자료구조의 구현 역시 선형 자료구조의 구현이 필요하다!
내일 그래프 코드 구현을 진행할 예정인데,
그 전에 아직 학습하지 않아 이해가 되지 않는 알고리즘 복잡도 계산과
스택, 큐의 구현을 먼저 복습해야겠다.